A sideways look at economics
All of us have, at some time, had the ‘pleasure’ of living with others, be that friends, family, lodgers or even the eclectic mix of individuals thrown together in first-year undergraduate dorms. Sharing accommodation can be great fun and I’m sure readers will all have plenty of anecdotes to recount. But, as with anything, there are drawbacks. Often chief among these are gripes about hygiene, bin rotas and, most commonly, who does the cleaning.
Bad roommates are just as bad as good ones are good — most memorable to me is one individual who left a half-cooked chicken in the sink, and another whose baking exploits lasted a full ten hours and simultaneously covered dining room, living room and kitchen in flour. Living with others is complex and such disagreements are two-a-penny. And yet, most people living in shared accommodation manage to keep their houses in an at least semi-presentable state.
So, how would an economist explain this? Well, textbooks might consider such situations through the lens of a simple game theory pay-off matrix. To understand how this would work, let’s assume there are two housemates, who each prefer the house to be clean.[1] However, not being Mary Poppins, they can’t simply click their fingers and tell the room to tidy itself. Instead, they suffer some cost if they do the cleaning themselves.
Under such a framework, the outcomes will vary according to each individual’s attachment to cleanliness and their distaste for doing the cleaning. Indeed, it can be shown that one housemate may do all the cleaning if their utility from cleaning is sufficiently large. Knowing this, the best strategy for all other housemates is to simply wait for the house to be cleaned.[2]

However, while such a model may be appealing for its visual simplicity, it does leave a lot to be desired. Chief among its limitations, is its assumption that cleaning is done in discrete amounts (that’s to say it’s either done or not done). In reality, this isn’t true and economic theory would predict that rational individuals will clean up to the point where the marginal benefit of further cleaning is equal to the marginal cost of doing so. We could, for example, express an individual’s decision over their cleaning effort as the solution to the following optimisation problem:
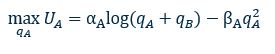
where UA is the utility obtained from a certain level of cleaning, αAand βA are parameters, and qA and qB reflect the amount of cleaning by person A and person B respectively.
Under this specification, each individual’s utility will depend not just upon their own level of effort, but also upon the amount of cleaning done by their housemate. What’s more, the benefit accruing from further cleaning decreases, and the additional effort required rises, as the quantity of cleaning increases.[3]
In line with the previous game theory framework, this model predicts that ‘lazy’ people (those with a higher marginal cost of effort) will tidy less while those most concerned with “keeping up appearances” will tend to clean more.[2] The outcome of this laissez faire system hardly seems fair and often proves a source of contention within households. But it’s fair from an economic perspective — those with a higher net gain from cleaning do more of it.
Those living in professional houseshares often attempt to resolve the unequal distribution of cleaning duties through outsourcing (i.e. employing a cleaner). While this may resolve some of the issues associated with the laissez faire system, it does introduce new questions. For example, should the cleaning costs be split evenly? From a theoretical standpoint the answer is most certainly no. Who pays more ought to depend upon who has more to gain from employing the cleaner.
You might think that this would be the person who’d been doing the majority of the cleaning before. And, most likely it would be. After all, if the only benefit is that a cleaner reduces labour effort then it seems logical to expect that this person has the most to gain. However, the burden of cleaning under the laissez faire system depends not only upon the quantity of cleaning but also upon the cost of each unit of cleaning. If a person cleans more, but finds it less costly to do so then employing a cleaner may actually eat into their surplus and make them worse off.[5]
So, what does this teach me about me? I’ve lived with many different people over the years and have typically ended up doing more than my fair share of housework. I always thought this meant that I had a lower tolerance for mess than others. However, I‘ve never been in favour of hiring a cleaner. So, maybe my assertion was incorrect and I actually have a higher tolerance for mess than I previously thought. Or, maybe I was irrational in the past and should now change my behaviour. Who knows? Either way, economics has taught me something about myself. I’ve certainly got some self-reflection to do this weekend…
[1] Obviously, the house should be kept clean for hygienic reasons, but forward-looking individuals might also have an eye on reclaiming their deposit.
[2] The numbers shown in the table above are calculated such that person A values a tidy house at 8 whereas person B values it at 6 and that the cost of cleaning is 4 for both people (although this cost is split if both individuals clean). Under these assumptions, person B always has an incentive not to clean, regardless of person A’s actions. Knowing this, person A’s best response is to always do the cleaning. This is what’s commonly referred to as a Nash Equilibrium. However, such a result is highly sensitive to the size of each person’s pay-offs. Indeed, under different assumptions we could easily end up in the world of the so-called Prisoner’s Dilemma where neither player attempts to clean (the end result of this of course being a filthy house). The framework could also be specified in such a way that there could be gains if one person paid the other to do the cleaning.
[3] The formal solution to this model is such that . Disclaimer: please don’t attempt this at home as it’s likely result in tears (trust me, I’ve been there).
[4] Of course, individuals’ behaviour may also change over time. For instance, preferences may change significantly if one housemate is planning to invite friends over or if they have recently entered into a new relationship.
[5] If we assume that employing a cleaner ensures that the same amount of cleaning is done as in the laissez faire system, then it can be shown that person A may be cleaning more and still refuse to employ a cleaner while the person B cleans less but prefers to hire one. If the cost of the cleaner is evenly split then this result will occur if αA < αB (i.e. person B has a higher preference for cleanliness) and βA < βB (i.e. person A finds cleaning less onerous).