A sideways look at economics
According to data published earlier this month, the UK economy expanded by 0.5% in the month of February. That’s an impressive figure, particularly when you annualise it, as our friends across the pond tend to do. Annualising turns 0.5% into 6.2%! February’s growth estimate was much stronger than expected, beating the Reuters Poll consensus by 0.4 percentage points, in month-on-month terms, and that is what grabbed the headlines. But should it have done? How accurate are initial estimates of monthly UK GDP growth? Well, there’s good news and bad news.
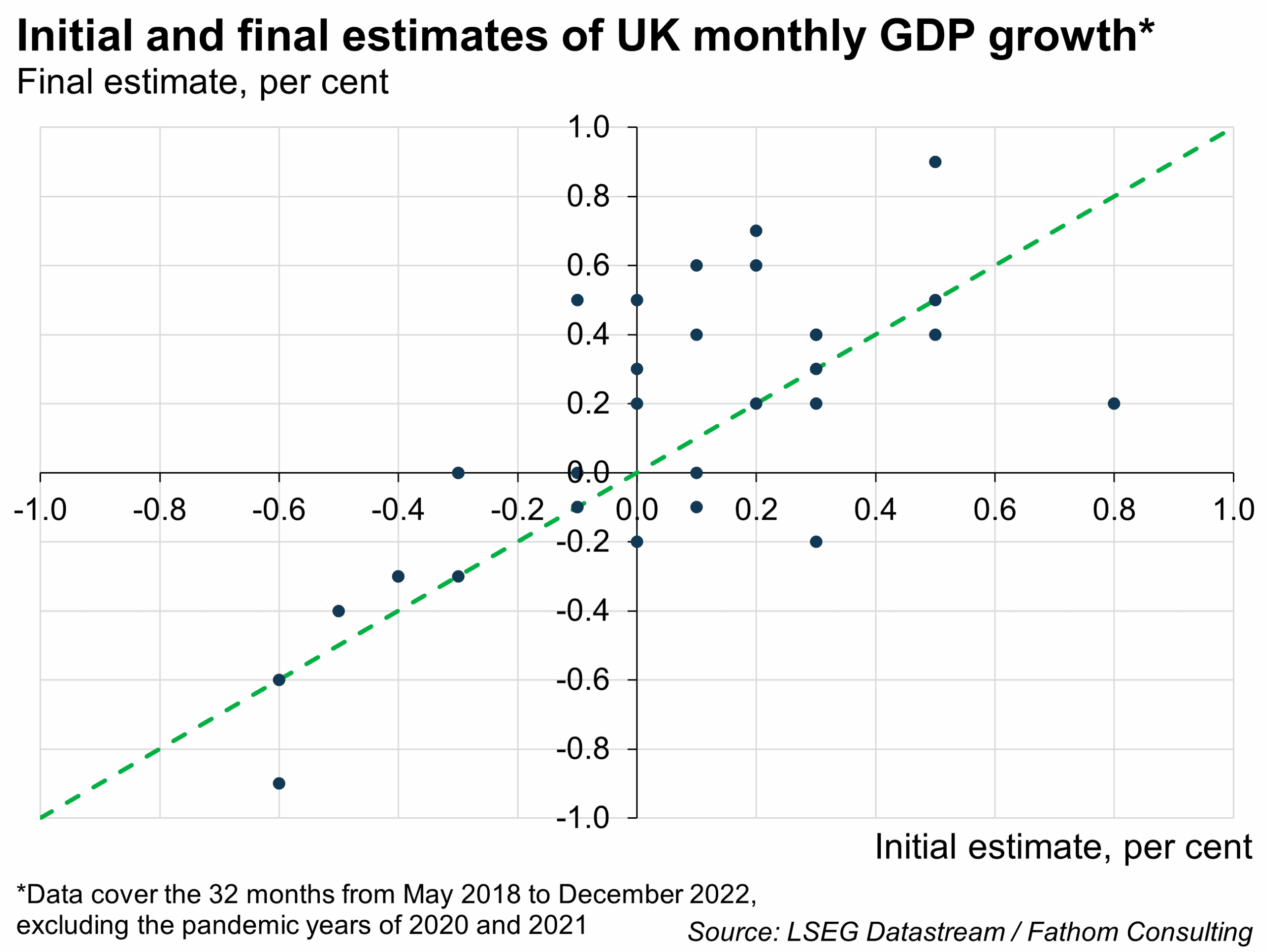
Let’s get the bad news out of the way first: they’re not terribly accurate. Our scatter plot compares the final estimate of monthly UK GDP growth (on the vertical axis) with the initial one (on the horizontal axis).[1] Most estimates lie quite some way from the 45-degree line, which would indicate a perfect first estimate. In fact, the standard error of the initial estimate is 0.3 percentage points. If revisions were normally distributed, that would mean we could not (yet) rule out the notion that economic forecasters got February right after all.
But what about the good news? The good news is that the initial estimates have at least improved, according to my simple definition. Some years ago, about the time that the ONS started to publish monthly estimates of GDP, I wrote a slightly cheeky blog post comparing the accuracy of quarterly estimates of UK GDP growth over the period 2003 Q3 to 2015 Q4 with what a monkey jumping around on a typewriter might have achieved.[2] I found that our fellow primate would have done slightly better. My reasoning was as follows. Over the 50 quarters included in my analysis, the ONS had got the initial estimate of quarterly GDP growth right just once. Over that same period, quarterly GDP growth had varied from -2.2% to +1.5%. By convention, the ONS published growth estimates to one decimal place, which gave us 38 numbers to choose from. Our random number generator would have got it right with a 1-in-38 chance on each of the 50 guesses, giving an expected number of correct guesses of 1/38 * 50 or about 1.3. The monkey, in other words, would have done 30% better than the statistician. But look how times have changed. Over the period from May 2018 to December 2022, but excluding the pandemic months, the initial estimate of monthly GDP growth proved to be spot on six times. Applying the same logic as before, that is 3.5 times better than our random number generator.[3] There appears to be useful information in the initial estimates of monthly UK GDP growth after all!
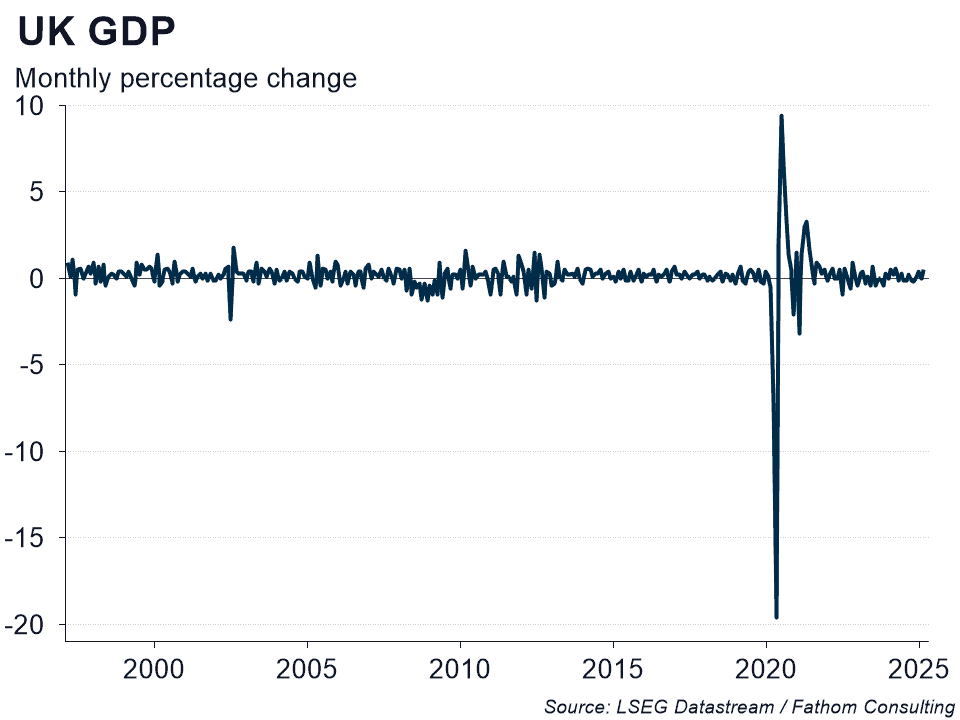
I will close with the chart above. Monthly UK GDP growth is a noisy series. In contrast to its quarterly cousin, it has no persistence. Quite the reverse in fact. If you model monthly UK GDP growth as a function of a constant term and its lag, the coefficient on the lag is -0.3.[4] The stronger monthly UK GDP growth is this month, the weaker it will be next month. Maybe the UK economy is genuinely erratic in this way, or maybe the ONS simply fails to remove the noise. Either way, pity the poor economist struggling to predict the next twist and turn in monthly UK GDP growth!
[1] We consider estimates of GDP growth to be ‘final’ once the National Accounts have been balanced so that all three approaches to estimating GDP (output, income, and expenditure) give the same answer. The National Accounts have been balanced up to 2022, so we exclude all estimates of GDP growth beyond 2022 from our chart. Also, to be fair to the ONS, we exclude the pandemic period, which we (generously) take to include all of 2020 and 2021.
[2] This is the monkey of ‘infinite monkey theorem’ fame – effectively a metaphor for a random number generator.
[3] Over the period shown in the chart, the final estimate of UK monthly GDP growth has varied from -0.9% to +0.9%, giving 19 numbers to choose from. The random number generator should have been expected to get 1/19 * 32 = 1.7 of the guesses correct.
[4] This is not just a consequence of extreme volatility through the pandemic period.
More by this author