A sideways look at economics
Everyone’s talking about inflation right now. With US consumer prices rising 4% in the year to April, it’s not hard to see why. Ask the general public what they think of this and they’ll probably succinctly conclude that higher prices are a bad thing. If you asked a typical economist for their views, what kind of answer do you think you’d get?
Well, for a start, it’s unlikely it would be succinct. But, if you did finally extract an answer from them, they’d probably proclaim something like this:
“A little inflation is probably good, but not too much (that’d be bad) and not too little (that’d also be bad) and we definitely don’t want to see falling prices (that’d be very, very bad).”
If you then pressed them to tell you the appropriate level of inflation, they’d probably start to spout about expectations, liquidity traps and effective lower bounds, eventually leaving you (and probably themselves) utterly bamboozled. However, there’s more than one type of inflation and today we’re here to talk about another kind — grade inflation.
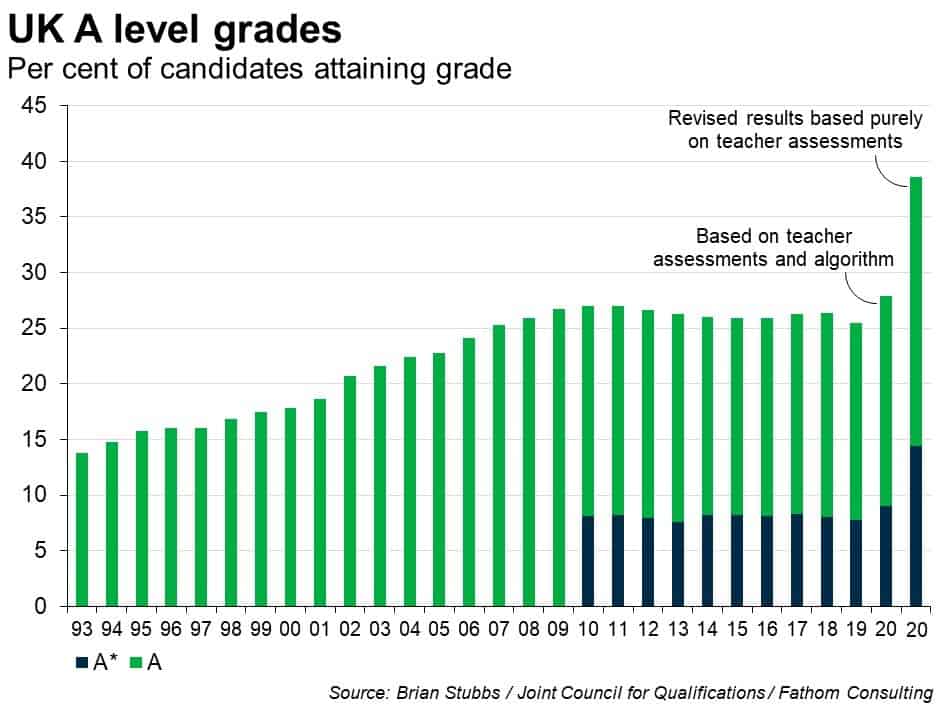
We’ve all been through school and we’ve all sat exams. We’re also probably all accustomed to the patronising phrase “Oh well, they were harder in my day”. Maybe they were (and maybe they weren’t) but want d’ya want kids to do about it? Should they demand harder exams? In the UK, debates about grade inflation came to a head after last summer’s exam fiasco.
As with many things, education was heavily disrupted by the pandemic and, as a result, exams were cancelled with teachers asked to grade pupils instead. However, Ofqual then spooked itself with concerns over grade inflation, and hoped to correct this via a machine-learning algorithm. I’m not going to comment on the flaws in that algorithm (quite frankly, I don’t have the time, energy and word count). All I’ll say for now is that the algorithm took a small problem (grade inflation) and replaced it with several much larger ones (unfairness, discrimination and emotional turmoil). As George Box once said,
“Since all models are wrong the scientist must be alert to what is importantly wrong. It is inappropriate to be concerned about mice when there are tigers abroad.”
Indeed, one can even question whether it was necessary to lean against grade inflation at all.
In economics, signalling theory asserts that individuals already possess ability and that grading serves simply as a means to demonstrate this to potential employers.[1] From this point of view, the potential inflation of last year’s grades shouldn’t have been concerning.[2] How so? Well, let’s imagine that teachers were asked only to provide a mark (and not a grade) for each pupil. These could’ve been biased towards the upside. For argument’s sake, let’s assume they were inflated by five percentage points for all students. Arguably this wouldn’t have mattered, provided the relative ordering was preserved (something that definitely would’ve happened within classes, and probably across them too).[3] Had students been scored relatively (effectively by their percentile) in this manner, universities and employers could still have identified the best students. If you were an exam board clinging to the ideology of lettered grades, you could still have assigned them by retrospectively setting thresholds which would’ve allowed for comparisons with previous years’ grades.
Of course, that doesn’t mean that there wouldn’t have been costs had we seen rampant grade inflation in the short run. If the temporary system had led to teachers effectively competing with each other to offer higher and higher marks, then there would’ve been a far greater risk of misallocation of grades between students. The purpose of that algorithm was clearly to prevent this (though in the event, it was poorly executed and unnecessary). Truthfully, this was probably unlikely to have been a serious concern, given the implications for a teacher’s credibility had they acted this way.
However, even though we did see grade inflation last year, it probably won’t matter much in the long run. Over time, the grade competition between cohorts decreases as employers increasingly focus more on comparisons in recent achievements (higher levels of education, work experience etc.). In other words, the long-run impact of a one-off shock to average grades will be fairly small. And that’s the thing with grade inflation. As long as it doesn’t affect learning, and provided it doesn’t reduce the clarity of the grading system, it really doesn’t matter all that much.
[1] Of course, there are other motives for education. From an economic perspective, chief among these is human capital theory which suggests that the primary purpose of education is to boost your own capabilities thus raising your value to future employers and the amount they’d be willing to pay you. At a macro level, this will boost the productive potential of the economy. However, from a human capital perspective, grade inflation last summer would have been irrelevant since teaching had already been completed.
[2] From a signalling perspective, the effects of grade inflation largely depends upon how grades are assigned. If a pre-determined mark out of one hundred earns you a certain grade, then inflation is clearly bad as it lessens the signal that a grade sends, reducing its usefulness to employers. If, on the other hand, awards are determined by percentile scores (i.e. where your mark sits relative to that of others), then the top 10% will probably always be the top 10%, regardless of how easy the exams are. In other words, grade inflation will be immaterial.
[3] In truth, there may have been some cases where individual teachers excessively inflated grades. Consequently, it would’ve made sense to develop a way of spotting cases that warranted further investigation, maybe by looking at how classes performed relative to normal (this in itself is a very basic algorithm). However, the mistake of the Ofqual algorithm was twofold: 1) it was being used to reassign grades in an extremely large proportion of cases rather than for simply flagging those requiring checking by the exam board and 2) by adjusting for characteristics such as class size, it was embedding variables that teachers had already accounted for in their predictions, effectively double counting.