A sideways look at economics

Occasionally when we’re apart my girlfriend and I send each other little emoji kisses by text. Very cute and romantic, I know. A normal person would accept this situation, embrace it and continue to enjoy it. But one day my brain, as if controlled by some sort of economist God, got the better of me and I began wondering whether by texting too many kisses, we were lowering the value of a kiss. So I suggested that we restrict supply — was that a good idea?

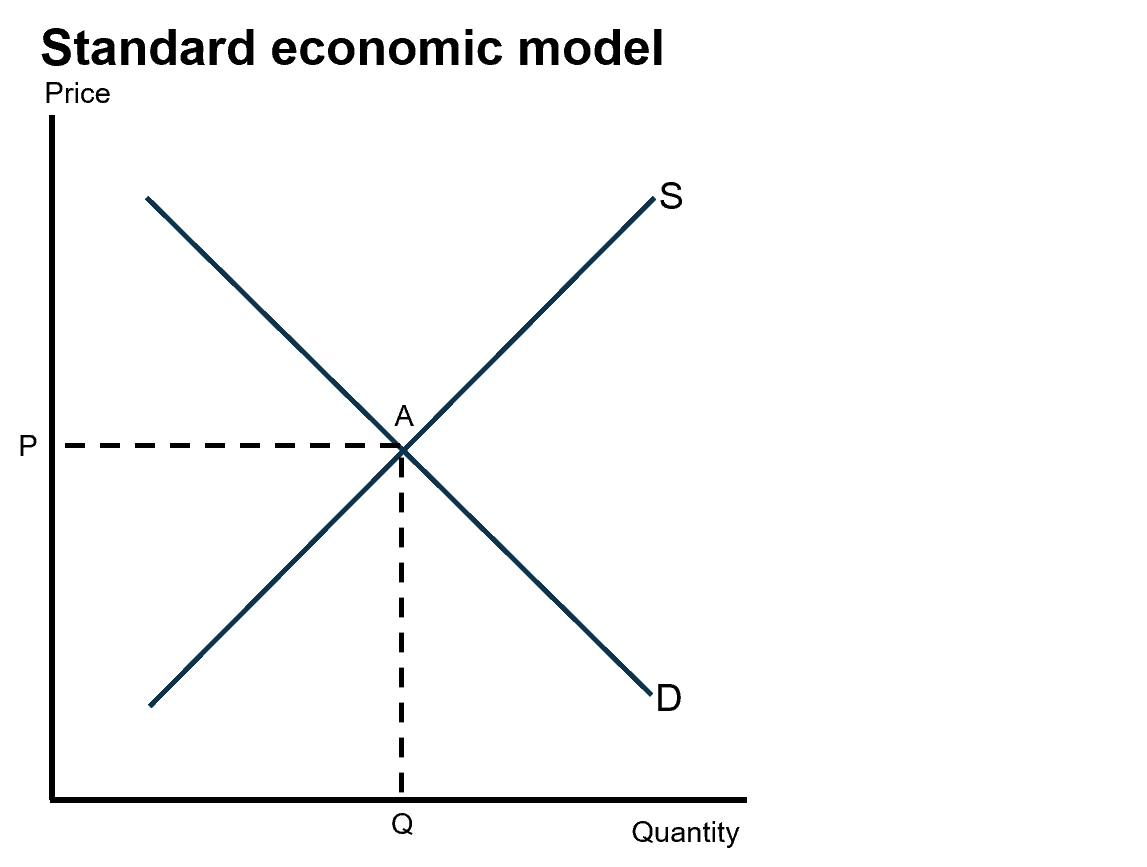
Well, no, she wasn’t sold on the idea. But that’s not to say that there may not be an economic rationale for this, so I decided to investigate. The laws of supply and demand are as old as the economics profession itself. Remember the chart below from A-level economics? The demand curve slopes down from top left to bottom right, and the supply curve slopes up from bottom left to top right. The curves intersect at point A, giving a market clearing price of P and a quantity supplied of Q.

But hang on. We don’t charge each other for kisses and we don’t even barter kisses either — a kiss in exchange for washing the dishes? No. So I tore up that diagram and started again. I came up with the modified kiss model, illustrated below.

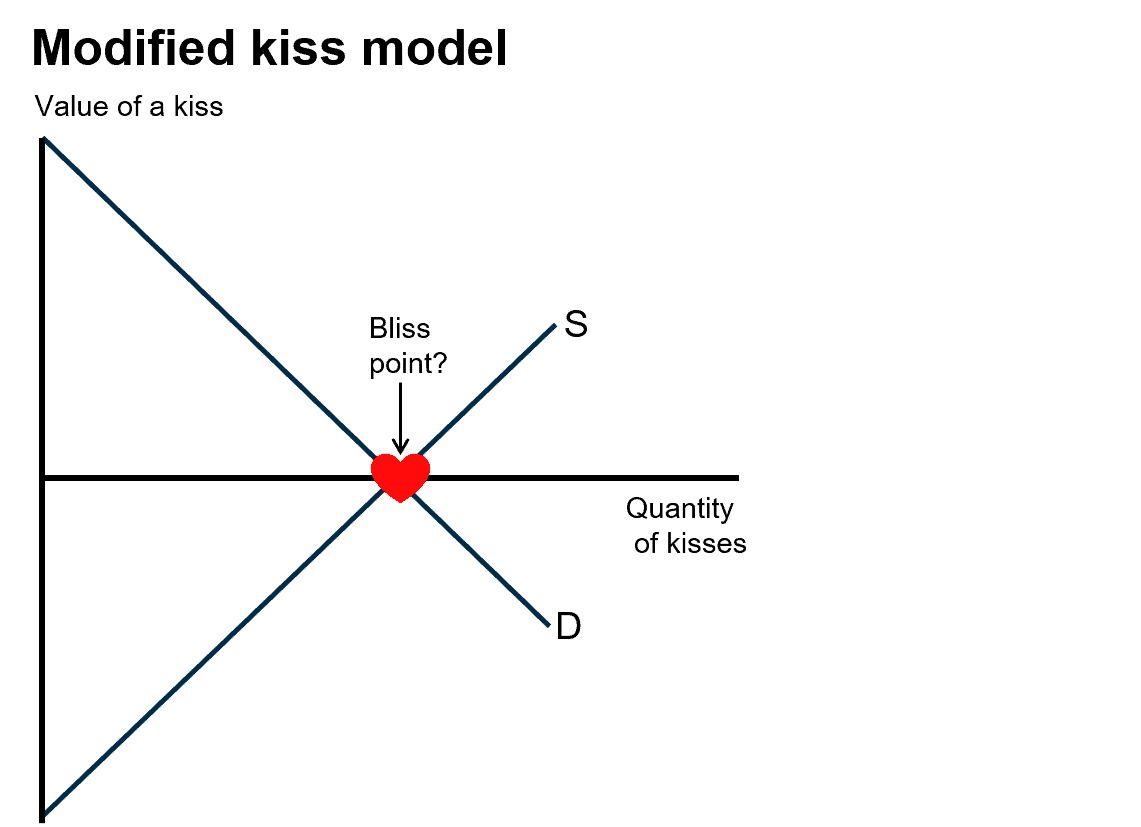
Here the supplier (let’s say me), gains positive value from giving my girlfriend a kiss. The supply curve, in effect, starts off below the origin since I get a lot of value from kissing her, at least up to a point. And since she also gets value from kissing me, up to a point, her demand curve slopes down. Luckily for us, our supply and demand curves intersect where the price, or value, we associate with kisses is zero. That’s because we’re perfectly matched. In other words, the market clearing equilibrium lies along the horizontal axis. Welfare is maximised, no money changes hands and nobody experiences any disutility from kissing. Bliss.

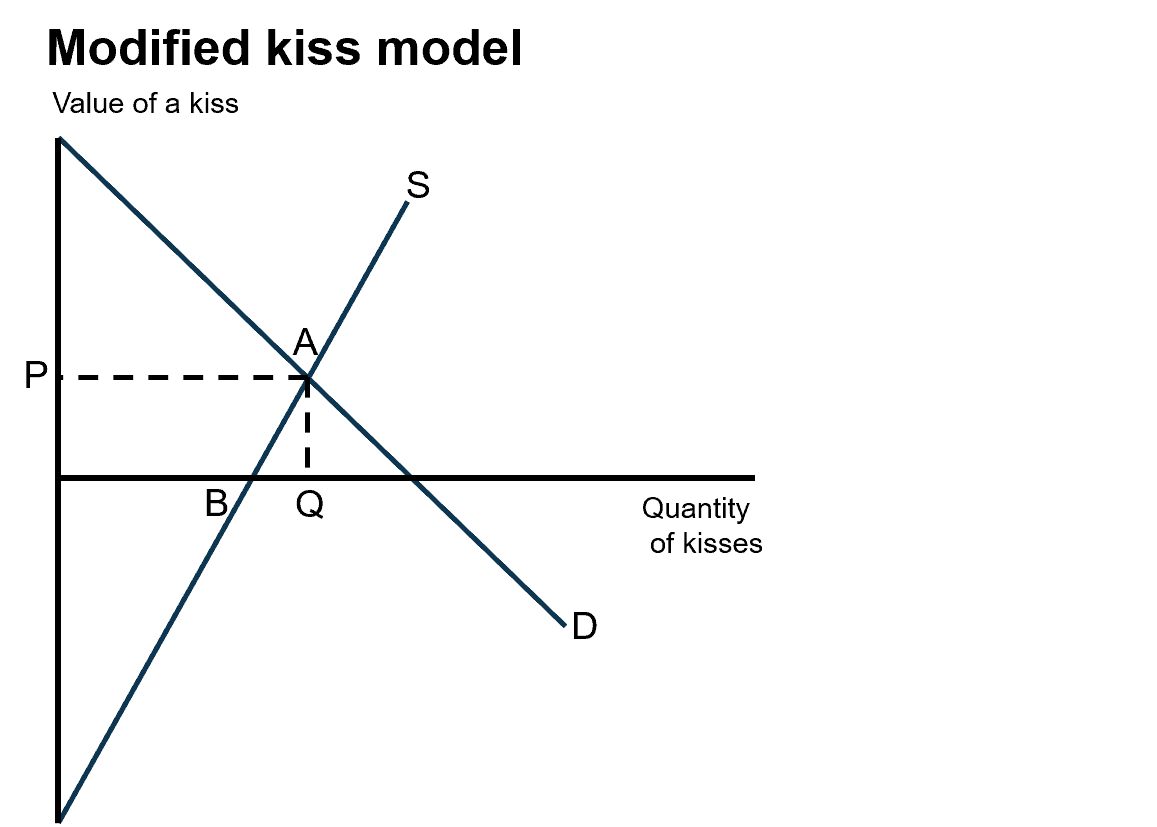
Not all couples are so fortunate, of course. In the diagram above, one half of the partnership — the supplier — is more rapidly sated by the act of kissing than her partner. The efficient solution lies at point A, with quantity of kisses supplied Q, at a price P. But there’s a constraint, unfortunately. Money can’t change hands, which means we’re left with an inefficient outcome at point B. The unfortunate demander is left wanting more, but can’t pay for it. They can ask for it, but this would come at a cost to the supplier and it would be an undesirable outcome for them. In this case, someone will end up experiencing some disutility from some of those kisses.

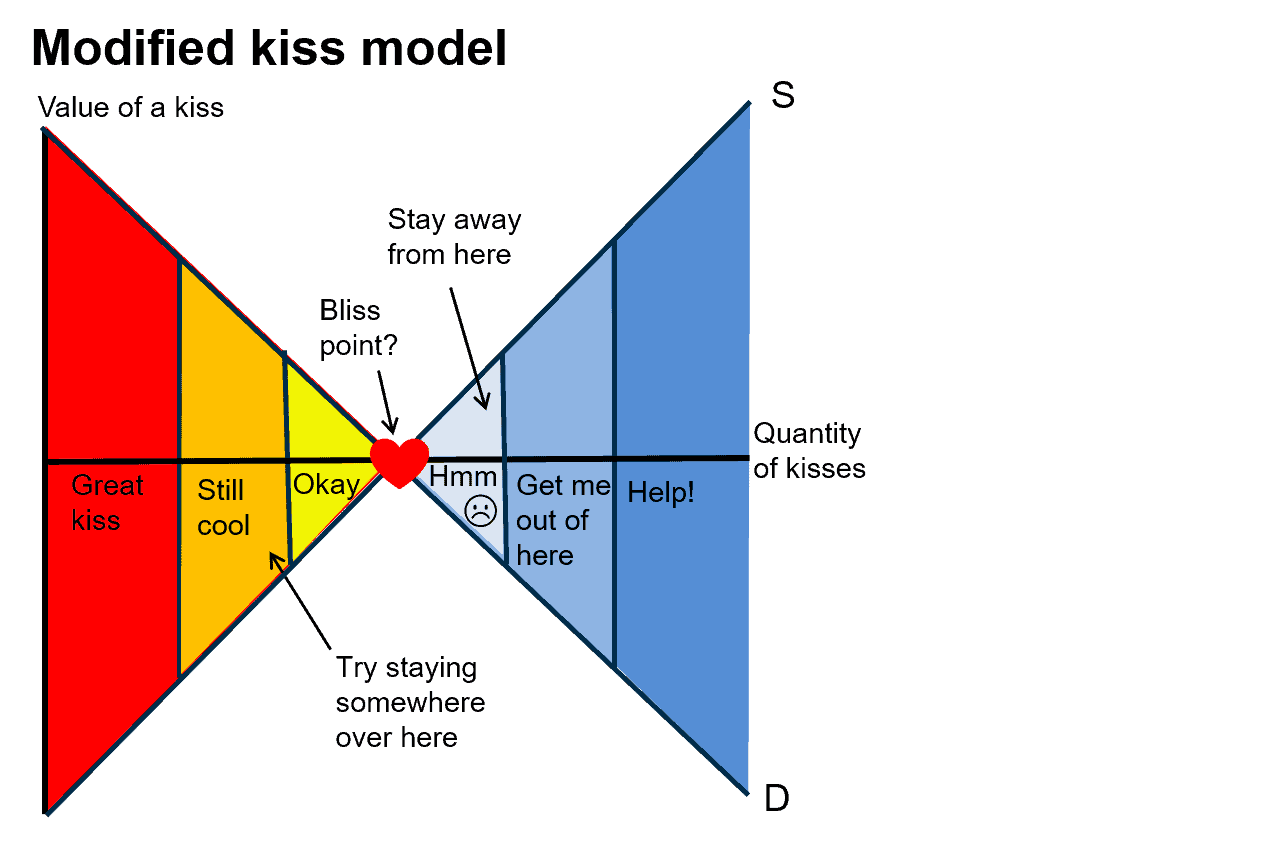
The bottom line is that I think my initial suggestion to put a cap on kisses is an important consideration for all couples, and not only in the scenario described above. Even in the scenario where couples are perfectly matched, the cap makes sense. There’s always a point where both partners are indifferent between having a kiss and not having a kiss. In economics jargon this might be referred to as the bliss point. But kissing when you’re completely indifferent between kissing and not kissing doesn’t really sound like bliss to me and this situation ought to be avoided.

Not only is kissing when you are completely indifferent to kissing not cool, but when you get close to the bliss zone, there’s little margin for error. A kiss too far and you would enter some dangerous territory, where one, or both partners experience disutility. Avoid the right side of the bliss point at all costs! The bottom line: keep to the left and keep some kisses in reserve.